Travel Salesman Problem Algorithm - Travelling Salesman Problem Dynamic Programming Graph Theory Youtube
This problem is soluble for smaller number n of cities but it breaks down as the number of cities grows. Both of the solutions are infeasible.

A 4 5 Approximation Algorithm For The Maximum Traveling Salesman Problem Springerlink
Lösung des Traveling Salesman Problem mit dem Genetischen Algorithmus.
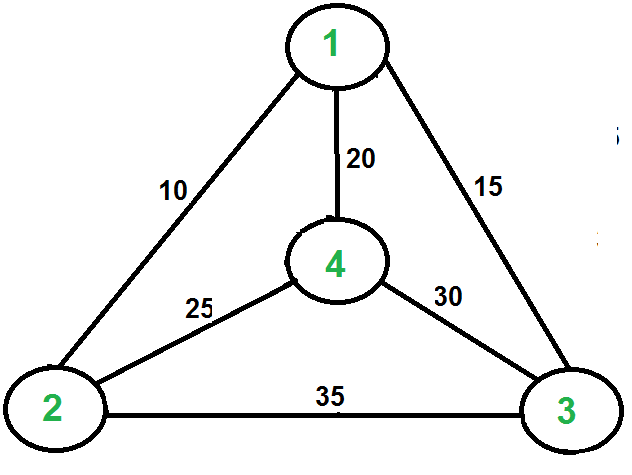
Travel salesman problem algorithm. Travel Salesman Problem is one of the most known optimization problems. Multiple variations on the problem have been developed as well such as mTSP a generalized version of the problem and Metric TSP a subcase of the problem. What is the travelling salesman problem.
For n number of vertices in a graph there are n - 1. Travelling Salesman Problem is based on a real life scenario where a salesman from a company has to start from his. The time to examine a single path is.
Die Implementierung ist keine typische Python-Implementierung. There are approximate algorithms to solve the problem though. One such problem is the Traveling Salesman Problem.
Travelling salesman problem is the most notorious computational problem. A salesperson has to visit multiple cities on their trip. We use a genetic algorithm to find the shortest route.
Say it is T 1234 means initially he is at village 1 and then he can go to any of 234. Given a list of cities and the distances between each pair of cities what is the shortest possible route that visits each city and returns to the origin city. Finding the best solution to a problem from a finite set of possible solutions.
Mlrose provides functionality for implementing some of the most popular randomization and search algorithms and applying them to a range of different optimization problem domains. In this tutorial we will discuss what is meant by the travelling salesperson problem and step through an example of how mlrose can be used to solve it. University of Pittsburgh 2013 Although a global solution for the Traveling Salesman Problem does not yet exist there are algorithms for an existing local solution.
This is the second in a series of three tutorials about. The traveling salesman problem TSP involves finding the shortest path that visits n specified locations starting and ending at the same place and visiting the other n. Instead of brute-force using dynamic programming approach the solution can be obtained in lesser time.
Although we havent been able to quickly find optimal solutions to NP problems like the Traveling Salesman Problem good-enough solutions to NP problems can be quickly found 1. While an optimal solution cannot be reached non-optimal solutions approach optimality and keep running time fast. TSP Algorithms and heuristics.
These algorithms can be implemented to find a solution to the optimization problems of various types. If there are n-cities the number of different paths among them is n-1. The traveling salesman problem TSP asks the following question.
We introduced Travelling Salesman Problem and discussed Naive and Dynamic Programming Solutions for the problem in the previous post. We can use brute-force approach to evaluate every possible tour and select the best one. For the visual learners heres an animated collection of some well-known heuristics and algorithms in action.
In this article we will briefly discuss about the Metric Travelling Salesman Probelm and an approximation algorithm named 2 approximation algorithm that uses Minimum Spanning Tree in order to obtain an approximate path. There are also necessary and su cient conditions to determine if a possible solution does exist when one is not given a. THE TRAVELING SALESMAN PROBLEM Corinne Brucato MS.
Here problem is travelling salesman wants to find out his tour with minimum cost. Der in diesem Abschnitt beschriebene Python Code ist im Modul geneticAlgopy zusammengefasst. It is a classical problem in graph theory.
IngsalesmanproblemThesetofalltoursfeasiblesolutionsis broken upinto increasinglysmallsubsets by a procedurecalledbranch- ingFor eachsubset a lowerbound onthe length ofthe tourstherein. In fact there is no polynomial-time solution available for this problem as the problem is a known NP-Hard problem. It has no closed analytic and algorithmic solution.
The original Traveling Salesman Problem is one of the fundamental problems in the study of combinatorial optimizationor in plain English. From there to reach non-visited vertices villages becomes a new problem. The problem says that a salesman is given a set of cities he has to find the shortest route to as to visit each city exactly once and return to the starting city.
Travelling Salesman Problem Dynamic Programming Graph Theory Youtube
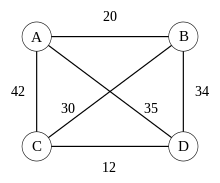
Travelling Salesman Problem Wikipedia
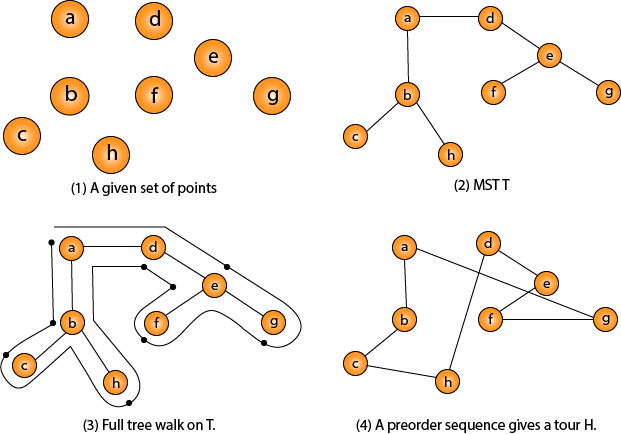
Daa Travelling Salesman Problem Javatpoint
Traveling Salesman Problem Dynamic Programming Approach Baeldung On Computer Science

Travelling Salesman Notes And Video A Minimum Of Blind Calculation

0 Traveling Salesman Problem Download Scientific Diagram

Travelling Salesman Problem Set 1 Naive And Dynamic Programming Geeksforgeeks

Swap Based Discrete Firefly Algorithm For Traveling Salesman Problem Springerlink

Solving Travelling Salesman Problem Using Firefly Algorithm
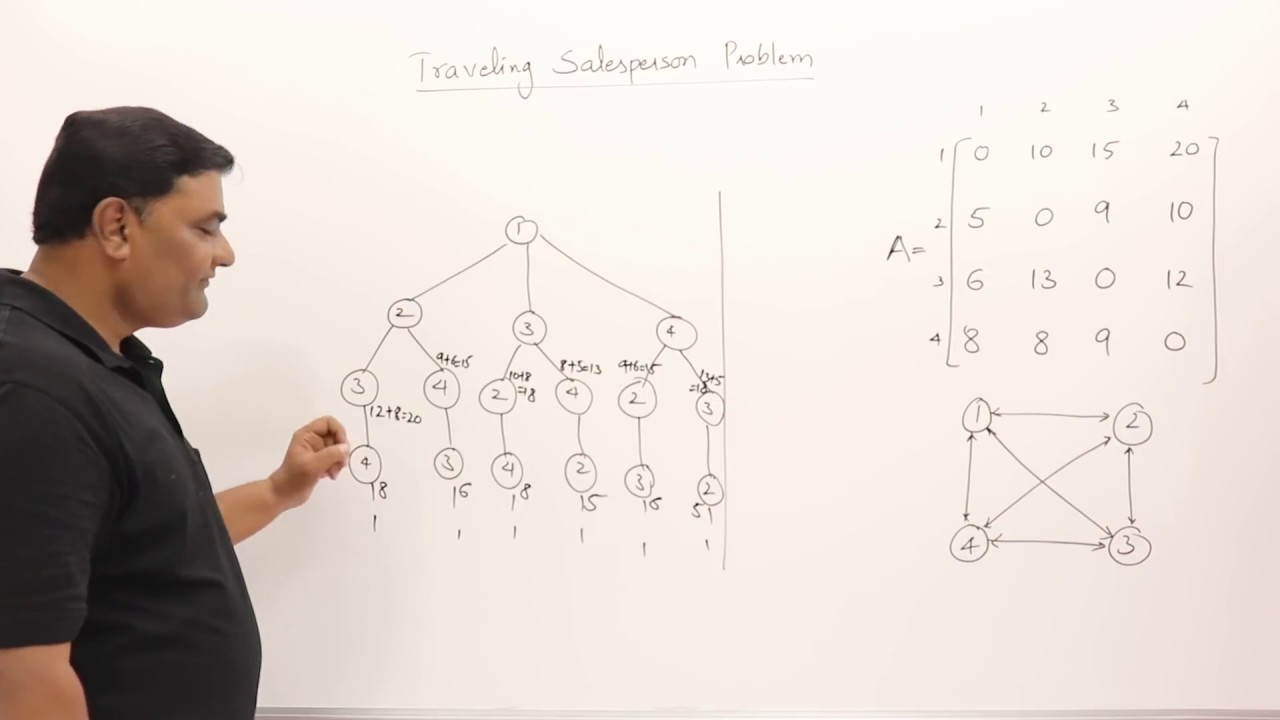
4 7 Traveling Salesperson Problem Dynamic Programming Youtube

Travelling Salesman Problem Wikipedia

Figure 1 From New Genetic Algorithm For The Travelling Salesman Problem Semantic Scholar

Fast Marching Methods For The Continuous Traveling Salesman Problem Pnas
Using A Genetic Algorithm For Traveling Salesman Problem In Python Cresco
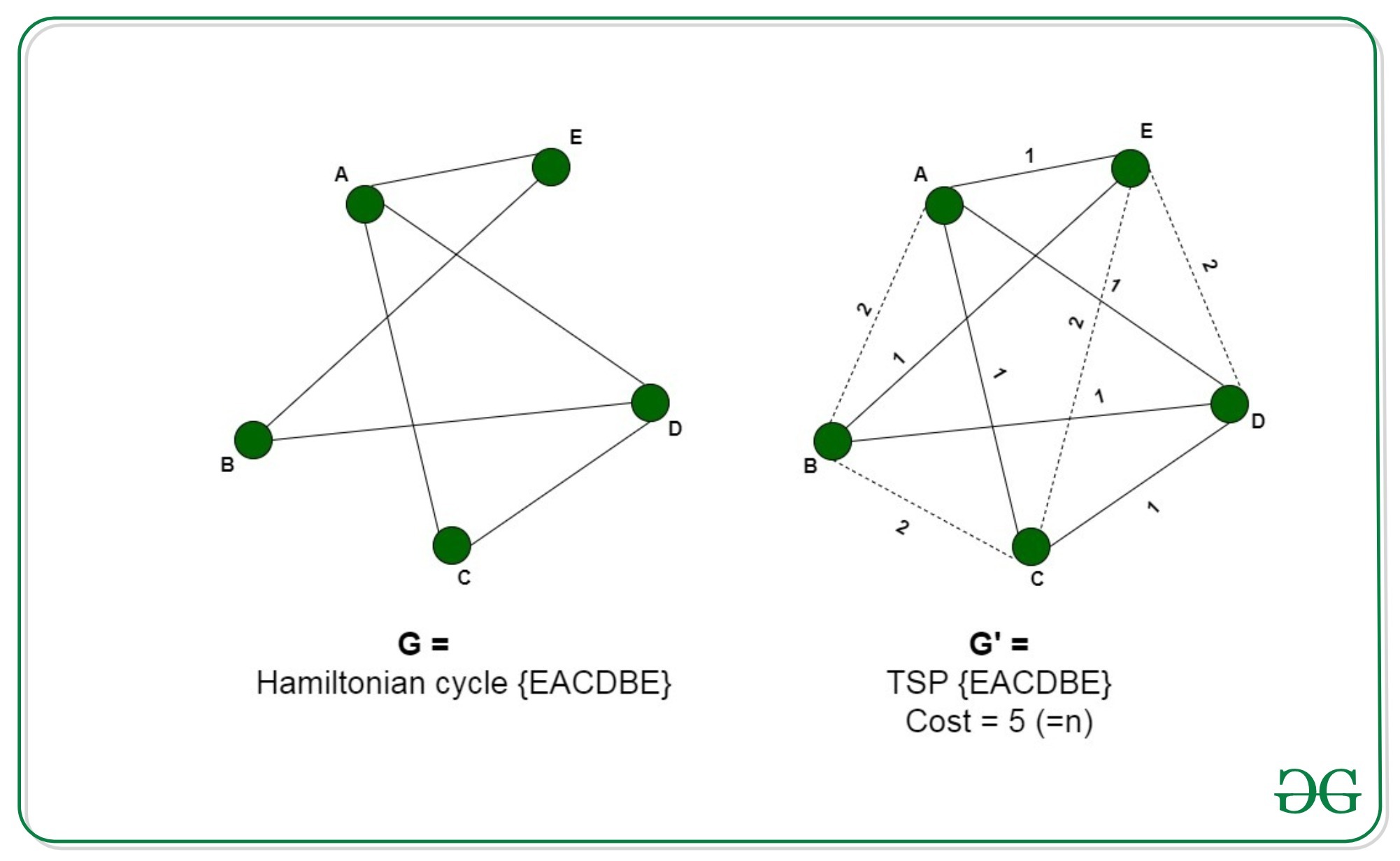
Proof That Traveling Salesman Problem Is Np Hard Geeksforgeeks

Suggestions For Speeding Up A Dynamic Programming Solution To The Traveling Salesman Problem Stack Overflow
Are You Ready For Solving The Traveling Salesman Problem By Jimmy Shen Analytics Vidhya Medium